Metrike za evaluaciju klasifikatora

ROC (engl. receiver operating characteristic)
- krivulja koja pokazuje odziv (TPR) kao funkciju fall-outa (FPR).
- Model koji radi nasumičnu klasifikaciju nalazit će se na pravcu TPR=FPR, bolji model će biti iznad, a lošiji ispod tog pravca.
AUC (engl. area under curve) - površina ispod ROC krivulje - veća površina znači bolji model.

F mjera¶

Harmonijska sredina između preciznosti i odziva. F1 mjera

F_1 = 2 \cdot \frac{1}{\frac{1}{precision} + \frac{1}{recall}} = 2 \cdot \frac{precision \cdot recall}{precision + recall}

(6)

Općenito Fβ mjera

F_\beta = \frac{(1 + \beta^2) \cdot precision \cdot recall}{\beta^2 \cdot precision + recall}

(7)

β < 1 - preciznost je važnija (za β=0.5 je preciznost dvaput važnija od odziva)
β > 1 - odziv je važniji (za β=2 je odziv dvaput važniji od preciznosti)

Zašto se koristi harmonijska sredina?

Jednako bi se mogla koristiti i aritmetička $\frac{(a_1 + a_2 + a_3 + \dots + a_n)}{n}$ ili geometrijska sredina $\sqrt[n]{a_1 \cdot a_2 \cdot a_3 \dots a_n}$
Harmonijska sredina se nameće kao najstroža - pesimistična procjena - ako je jedna od vrijednosti mala, rezultat će biti blizu te vrijednosti
Primjer: za 3 i 9
- Aritmetička: 6
- Geometrijska: 5.196
- Harmonijska: 4.5

import textwrap
from sklearn.metrics import get_scorer_names, classification_report

print(textwrap.fill(str(get_scorer_names())))

['accuracy', 'adjusted_mutual_info_score', 'adjusted_rand_score',
'average_precision', 'balanced_accuracy', 'completeness_score',
'd2_absolute_error_score', 'explained_variance', 'f1', 'f1_macro',
'f1_micro', 'f1_samples', 'f1_weighted', 'fowlkes_mallows_score',
'homogeneity_score', 'jaccard', 'jaccard_macro', 'jaccard_micro',
'jaccard_samples', 'jaccard_weighted', 'matthews_corrcoef',
'mutual_info_score', 'neg_brier_score', 'neg_log_loss',
'neg_max_error', 'neg_mean_absolute_error',
'neg_mean_absolute_percentage_error', 'neg_mean_gamma_deviance',
'neg_mean_poisson_deviance', 'neg_mean_squared_error',
'neg_mean_squared_log_error', 'neg_median_absolute_error',
'neg_negative_likelihood_ratio', 'neg_root_mean_squared_error',
'neg_root_mean_squared_log_error', 'normalized_mutual_info_score',
'positive_likelihood_ratio', 'precision', 'precision_macro',
'precision_micro', 'precision_samples', 'precision_weighted', 'r2',
'rand_score', 'recall', 'recall_macro', 'recall_micro',
'recall_samples', 'recall_weighted', 'roc_auc', 'roc_auc_ovo',
'roc_auc_ovo_weighted', 'roc_auc_ovr', 'roc_auc_ovr_weighted',
'top_k_accuracy', 'v_measure_score']

import numpy as np
from sklearn import neighbors
from sklearn import metrics
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import seaborn as sns

iris = load_iris()
x = iris.data
y = iris.target

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=1/3, random_state=42)

algorithm = neighbors.KNeighborsClassifier(n_neighbors=3)
model = algorithm.fit(x_train, y_train)
predictions = model.predict(x_test)

cm = metrics.confusion_matrix(y_test, predictions)

print(cm)

[[19  0  0]
 [ 0 15  0]
 [ 0  1 15]]

fix, ax = plt.subplots(1, 1, figsize=(4, 4))
cm = metrics.confusion_matrix(y_test, predictions)
ax = sns.heatmap(cm, annot=True, square=True, xticklabels=iris.target_names, yticklabels=iris.target_names)
ax.set_xlabel("Predicted")
ax.set_ylabel("Actual")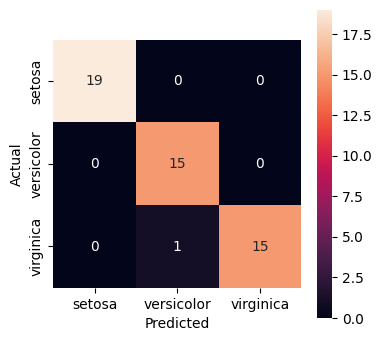

macro_precision = metrics.precision_score(y_test, predictions, average='macro')
print("Macro precision is:", macro_precision)

Macro precision is: 0.9791666666666666

macro_precision_1 = (np.diag(cm)/cm.sum(axis=0)).sum() / len(iris.target_names)
print(macro_precision_1)

0.9791666666666666

micro_precision = metrics.precision_score(y_test, predictions, average='micro')
print("Micro precision is:", micro_precision)

Micro precision is: 0.98

report = metrics.classification_report(y_test, predictions, target_names=iris.target_names)
print(report)

              precision    recall  f1-score   support

      setosa       1.00      1.00      1.00        19
  versicolor       0.94      1.00      0.97        15
   virginica       1.00      0.94      0.97        16

    accuracy                           0.98        50
   macro avg       0.98      0.98      0.98        50
weighted avg       0.98      0.98      0.98        50